Sometimes, there are more than one way to solve a problem. We need to learn how to compare the performance different algorithms and choose the best one to solve a particular problem. While analyzing an algorithm, we mostly consider time complexity and space complexity. Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Similarly, Space complexity of an algorithm quantifies the amount of space or memory taken by an algorithm to run as a function of the length of the input.
Time and space complexity depends on lots of things like hardware, operating system, processors, etc. However, we don't consider any of these factors while analyzing the algorithm. We will only consider the execution time of an algorithm.
Lets start with a simple example. Suppose you are given an array and an integer and you have to find if exists in array .
Simple solution to this problem is traverse the whole array and check if the any element is equal to .
for i : 1 to length of A
if A[i] is equal to x
return TRUE
return FALSEEach of the operation in computer take approximately constant time. Let each operation takes time. The number of lines of code executed is actually depends on the value of . During analyses of algorithm, mostly we will consider worst case scenario, i.e., when is not present in the array . In the worst case, the if condition will run times where is the length of the array . So in the worst case, total execution time will be . for the if condition and for the return statement ( ignoring some operations like assignment of ).
As we can see that the total time depends on the length of the array . If the length of the array will increase the time of execution will also increase.
Order of growth is how the time of execution depends on the length of the input. In the above example, we can clearly see that the time of execution is linearly depends on the length of the array. Order of growth will help us to compute the running time with ease. We will ignore the lower order terms, since the lower order terms are relatively insignificant for large input. We use different notation to describe limiting behavior of a function.
-notation:
To denote asymptotic upper bound, we use -notation. For a given function , we denote by (pronounced “big-oh of g of n”) the set of functions:
{ : there exist positive constants and such that for all }
-notation:
To denote asymptotic lower bound, we use -notation. For a given function , we denote by (pronounced “big-omega of g of n”) the set of functions:
{ : there exist positive constants and such that for all }
-notation:
To denote asymptotic tight bound, we use -notation. For a given function , we denote by (pronounced “big-theta of g of n”) the set of functions:
{ : there exist positive constants and such that for all }
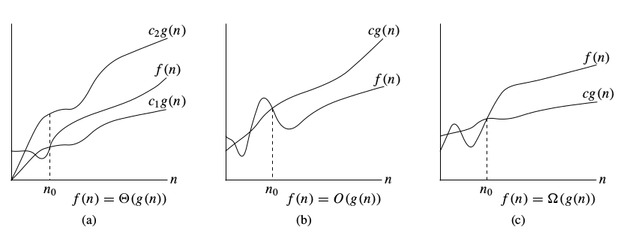
Time complexity notations
While analysing an algorithm, we mostly consider -notation because it will give us an upper limit of the execution time i.e. the execution time in the worst case.
To compute -notation we will ignore the lower order terms, since the lower order terms are relatively insignificant for large input.
Let
Lets consider some example:
1.
int count = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < i; j++)
count++;Lets see how many times count++ will run.
When , it will run times.
When , it will run times.
When , it will run times and so on.
Total number of times count++ will run is . So the time complexity will be .
2.
int count = 0;
for (int i = N; i > 0; i /= 2)
for (int j = 0; j < i; j++)
count++;This is a tricky case. In the first look, it seems like the complexity is . for the loop and for loop. But its wrong. Lets see why.
Think about how many times count++ will run.
When , it will run times.
When , it will run times.
When , it will run times and so on.
Total number of times count++ will run is . So the time complexity will be .
The table below is to help you understand the growth of several common time complexities, and thus help you judge if your algorithm is fast enough to get an Accepted ( assuming the algorithm is correct ).
| Length of Input (N) | Worst Accepted Algorithm |
|---|---|
A lot of students get confused while understanding the concept of time-complexity, but go below you will get in simple :
Imagine a classroom of 100 students in which you gave your pen to one person. Now, you want that pen. Here are some ways to find the pen and what the O order is.
O(n2): You go and ask the first person of the class, if he has the pen. Also, you ask this person about other 99 people in the classroom if they have that pen and so on,
This is what we call O(n2).
O(n): Going and asking each student individually is O(N).
O(log n): Now I divide the class into two groups, then ask: “Is it on the left side, or the right side of the classroom?” Then I take that group and divide it into two and ask again, and so on. Repeat the process till you are left with one student who has your pen. This is what you mean by O(log n).
I might need to do the O(n2) search if only one student knows on which student the pen is hidden. I’d use the O(n) if one student had the pen and only they knew it. I’d use the O(log n) search if all the students knew, but would only tell me if I guessed the right side.
NOTE :
We are interested in rate of growth of time with respect to the inputs taken during the program execution .
Another Example:
Time Complexity of algorithm/code is not equal to the actual time required to execute a particular code but the number of times a statement executes. We can prove this by using time command. For example, Write code in C/C++ or any other language to find maximum between N numbers, where N varies from 10, 100, 1000, 10000. And compile that code on Linux based operating system (Fedora or Ubuntu) with below command:
gcc program.c – o program
run it with time ./program
You will get surprising results i.e. for N = 10 you may get 0.5ms time and for N = 10, 000 you may get 0.2 ms time. Also, you will get different timings on the different machine. So, we can say that actual time requires to execute code is machine dependent (whether you are using pentium1 or pentiun5) and also it considers network load if your machine is in LAN/WAN. Even you will not get the same timings on the same machine for the same code, the reason behind that the current network load.
Now, the question arises if time complexity is not the actual time require executing the code then what is it?
The answer is : Instead of measuring actual time required in executing each statement in the code, we consider how many times each statement execute.


Thank you for your post. This is excellent information. It is amazing and wonderful to visit your site. For more info:- Xamarin App Development
ReplyDeletehttps://saglamproxy.com
ReplyDeletemetin2 proxy
proxy satın al
knight online proxy
mobil proxy satın al
İ3A4C